Übungsaufgaben
Aufgabe 1)
Der Graph der Funktion f(x)=(x-2)2 soll um 3 Einheiten nach links,
dann um 2 Einheiten nach unten geschoben werden. Wie lautet die Funktionsgleichung des neuen Graphen?
Lösung:
Wenn der Graph von f(x) um 3 Einheiten nach links verschoben werden soll,
so müssen wir f(x+3) bestimmen (nicht etwa f(x-3)!).
Überall wo im ursprünglichen Funktionsterm ein x steht, muss jetzt x+3 eingesetzt werden.
Dann ist g(x)=f(x+3)=((x+3)-2)2=(x+1)2.
Um die neue Funktion um 2 Einheiten nach unten zu schieben, bilden wir g(x)-2 und erhalten die Funktion
h(x)=(x+1)2-2.
Ergebnis: Die Funktionsgleichung der neuen Funktion lautet h(x)=(x+1)2-2.
Aufgabe 2)
Der Graph der Funktion f(x)=2x3-1 soll um 1 Einheit nach oben geschoben,
dann an der x-Achse gespiegelt und schließlich um 2 Einheiten nach rechts verschoben werden.
Wie lautet die Funktionsgleichung der neuen Funktion?
Lösung:
Wir bilden f(x)+1 und verschieben somit den Graphen um eine Einheit nach oben.
Damit ist g(x)=f(x)+1=2x3.
Nun soll g(x) an der x-Achse gespiegelt werden.
Dies erreichen wir durch Multiplikation des Funktionsterms mit -1 wodurch wir h(x)=-2x3 erhalten.
Die Verschiebung um 2 Einheiten nach rechts erreichen wir durch Bilden von h(x-2).
Somit haben wir schließlich k(x)=h(x-2)=-2(x-2)3.
Ergebnis: Die Funktionsgleichung der neuen Funktion lautet k(x)=-2(x-2)3.
Aufgabe 3)
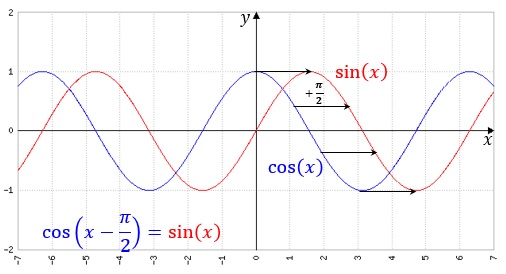
Durch welche geometrischen Operationen entsteht die Funktion g(x)=sin(x) aus der Funktion
f(x)=-cos(x-π/2)?
Lösung:
Zunächst wird f(x) an der x-Achse gespiegelt indem wir f(x) zu -f(x) machen. Aus
f(x) wird somit g(x)=cos(x-π/2). Diese Funktion ist gegenüber
der Kosinus-Funktion um π/2 nach rechts verschoben.
Wenn man aber cos(x) um π/2 nach rechts schiebt hat man bereits
die Sinus-Funktion. Wir sind somit schon am Ziel!
Abi-Aufgaben früherer Jahrgänge
Pflichtteil 2014 – Aufgabe 4
Gegeben sind die Funktionen f und g mit f(x)=cos(x) und
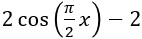 .
.a) Beschreiben Sie, wie man den Graphen von g(x) aus dem Graphen von f(x) erhält.
Lösung a):
• Verdopple die Amplitude, d.h. aus cos(x) wird 2cos(x).
• Ändere die Frequenz, d.h. aus 2cos(x) wird
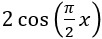 .
.• Verschiebe den Graphen um 2 Einheiten nach unten und erhalte g(x).
Pflichtteil 2011 – Aufgabe 4
Gegeben sind die Funktionen f und g mit f(x)=ex und g(x)=-e-x+2.
Beschreiben Sie, wie das Schaubild von g aus dem Schaubild von f entsteht.
Lösung a):
• Spiegeln von f an der y-Achse → g1(x)=e-x.
• Spiegeln von g1 an der x-Achse → g2(x)=-e-x.
• g2 in y-Richtung um 2 Einheiten nach oben schieben → g(x)=-e-x+2.
| Downloads |
PowerPoint